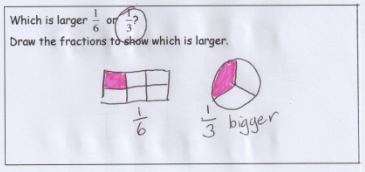Home > Topdrawer > Fractions > Misunderstandings > Different wholes > Shifting wholes
Shifting wholes
Examples of the misconception of using 'different wholes' can be seen in the diagrams that students use when comparing the size of two fractions.
In the following example, the student has correctly identified the larger fraction, but has not provided a logical reason.
Different shaped wholes.
The drawn response of two different shaped wholes suggests the student does not understand the need for the wholes to be the same, and is possibly just recalling familiar representations for these fractions.
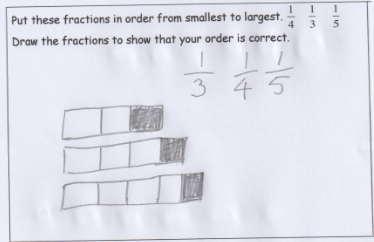
In the following example, the student has drawn a rectangle to illustrate the first fraction, then simply extended that whole to represent the second fraction.
Different length wholes.
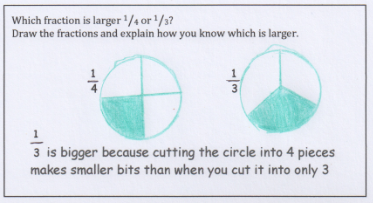
By contrast, this example demonstrates an awareness of the assumption that the wholes are the same. This understanding allows the reasoning about the size of the parts to develop.
Same sized wholes.
