Home > Topdrawer > Geometric reasoning > Good teaching > Exploring circles > Explore, predict, confirm
Explore, predict, confirm
Some of the circle geometry theorems are challenging for students to recognise.
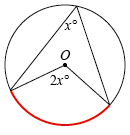
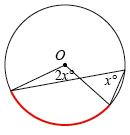
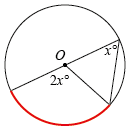
For example, in the case of angles at the centre and the circumference, most students easily recognise the theorem when presented with a diagram as that in Figure 1. However, many do not recognise Figures 2 or 3 as the same theorem. They need to understand that the angles must be subtended from the same arc. Marking the arc in colour is a good aid.
|
|
|
|
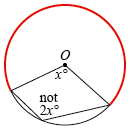
Furthermore, students frequently believe that Figure 4 is another case of the theorem. However, the angle at the centre subtended by the bigger arc is (360 – x) degrees, not x degrees, and therefore the angle at the circumference subtended by the same arc is half of that reflex angle.
Interaction with dynamic diagrams lets students explore multiple configurations of the same situation. It strengthens their visual skills while they are making and confirming their conjectures. It is also helpful to:
- have students work in pairs
- require students to write about the results in their own words
- follow up the investigations with class discussion
- provide exercises which utilise the theorems.
Circle geometry investigations
In this series of activities, students investigate a particular situation in a circle to form a hypothesis. They then further explore using dynamic geometry software.
Dynamic circle geometry
In this activity, pre-prepared learning objects allow all students to benefit from exploring dynamic circle geometry.