Home > Topdrawer > Fractions > Good teaching > Dividing > Fractions of collections
Fractions of collections
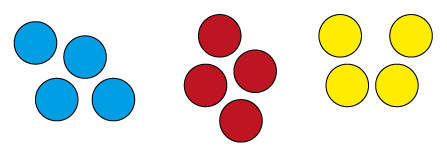
Finding one-third of a number is the same as dividing by three, and can be represented with materials in a similar way.
For example, \(\frac{1}{3}\) of 12 and 12 ÷ 3 could both be modelled using 12 counters partitioned into three equal groups of four.
Using 12 counters to model division.
The mathematical relations suggested by the three equal groups of four counters are:
| 3 \(\times\) 4 | = 12 |
| 12 ÷ 3 | = 4 |
| \(\frac{1}{3}\) of 12 | = 4 |
Working with fractions of collections is helped by a sound knowledge of factors and multiples.
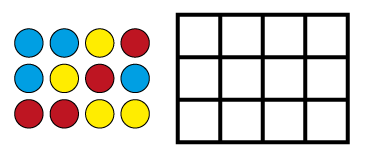
Using arrays and area grids strengthens the relationships between multiplication, division and fractions, by making the inverse relations more apparent.
An array of 12 and a grid of 12.
| 3 \(\times\) 4 | = 12 | 4 \(\times\) 3 | = 12 |
| 12 ÷ 3 | = 4 | 12 ÷ 4 | = 3 |
| \(\frac{1}{3}\) of 12 | = 4 | \(\frac{1}{4}\) of 12 | = 3 |
Fractions also appear in whole-number division when remainders occur.
For example, \(\frac{1}{3}\) of 13 (or 13 ÷ 3) results in 4 remainder 1. The remainder 1 can be partitioned into three equal parts and the sharing process continued, leading to the mixed-number answer \(4\frac{1}{3}\).
Using 13 counters to model division.
Part and wholes
Students develop strategies for working out the total number in a collection, given the number of items in the fractional part.
Divide it up
Sharing-as-division problems may give a result with a remainder. In some contexts it makes sense to divide the remainder into equal parts (fractions) and continue the sharing process.
