Home > Topdrawer > Fractions > Good teaching > Fraction sense > Fractions as numbers > Sequencing and counting
Sequencing and counting
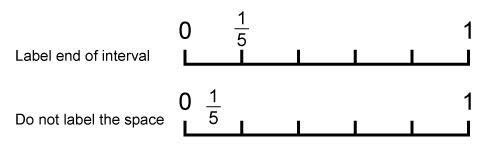
Students peg fraction cards (e.g. \(\frac{1}{5},\frac{2}{5},\frac{3}{5},\frac{4}{5},\frac{5}{5}\)) onto a rope marked with 0 at one end and 1 at the other, adjusting the spacing as needed to create equal intervals. Spacing can be checked by folding the rope.
Focus attention on the distance between 0 and 1 being the whole, and \(\frac{1}{5}\) being the unit of measure.
So \(\frac{1}{5}\) is one-fifth of the distance from 0 toward 1.
Highlight the fact that \(\frac{5}{5}\) is the same as 1.
Ask students to count forwards and backwards by fractions. This reinforces the idea that fractions are indeed numbers, each with their own position on a number line.
Correctly labelling number lines.
Change the labelling on the rope number line to extend from 0 to 2 or beyond, and ask students to locate fraction cards such as \(\frac{7}{5}\) or \(1\frac{2}{5}\).
Realising that improper fractions and mixed numbers extend fractions beyond 1 is an important part of understanding fractions as numbers.
Quarters pegged on a rope.
